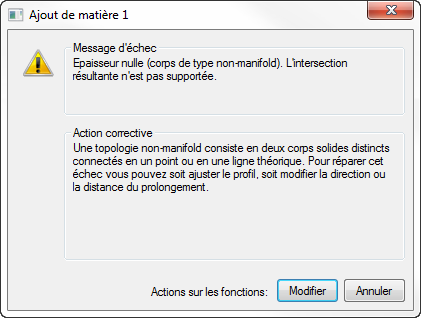
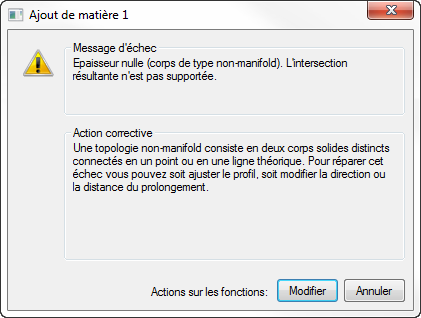
Ce guide apporte une explication détaillée à une situation que nombre d’entre vous connaissent : erreur de type «géométrie non manifold ». Cette erreur se produit en général lors d’ajout, d’enlèvement ou de booléen. Une manière simple d’expliquer cette erreur est que Solid Edge, à travers son noyau Parasolid, ne supporte pas les « épaisseurs nulles » dans un solide. Ces explications permettront de comprendre également certains problèmes de conversion d’un logiciel à l’autre.
Nous aborderons :
-
Le point de vue géométrique
-
Une question de « topologie »
-
La règle de Descartes-Euler
-
Les Corps non-manifold
-
Des différences entre modeleurs
Géométrie
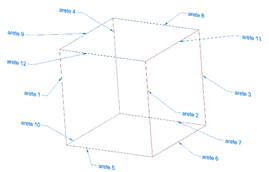
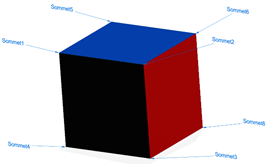
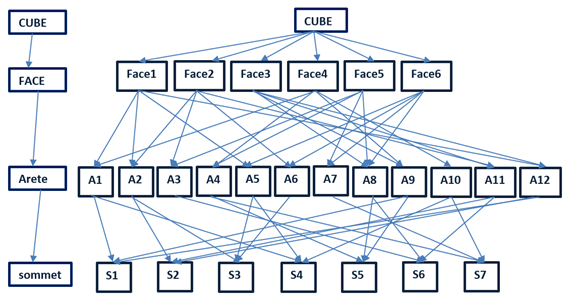
Abordons le problème d’un point de vue géométrique, au sens scientifique : Solid Edge représente un volume à partir d’information de base : faces, arêtes, sommets.
Les faces d’un volume partagent des arêtes et des sommets. Prenons un cube comme exemple simple d’information topologique :
Topologie
Une des branches des mathématiques traitant de la géométrie s’appelle la topologie. La topologie traite des relations de voisinage qui s’établissent entre des figures géométriques (quels sont les points communs entre les formes, comment on peut les regrouper), et qui ne sont pas altérées par la déformation des figures. Ainsi la topologie va regarder le nombre de faces, d’arêtes et de « trous » à l’intérieur d’un volume (si nous sommes en 3 dimensions).
L’application des principes de la topologie en CAO assure la cohérence des données géométriques lorsqu’on représente un volume à l’aide de ses frontières (faces, arêtes, sommets). La topologie élimine la redondance des entités pour un même volume (2 faces partageant une arête et 2 sommets par exemple, ne vont pas doubler l’arête partagée).
Les structures topologiques des principaux modeleurs géométriques sont très similaires :
-
Acis (Inventor/Autodesk, Acis/Dassault-Systèmes)
-
Parasolid (SolidWorks, Catia, Solid Edge, NX, Ansys, Femap, SolidThinking, etc…)
-
CGM (CATIA V5/ Dassault-Systèmes)
-
Granit (Pro Eng/PTC)
Les modeleurs demandent tous une géométrie cohérente. Par exemple, un volume solide ne peut se couper avec lui-même sans arête à l’intersection des surfaces. Attention, cette limitation, et les autres ci-dessous, ne s’appliquent pas lorsqu’on travaille avec des surfaces ! Seulement pour les volumes. Un cas célèbre est la bouteille de Klein :
Défi : modéliser cette bouteille en CAO !

Bouteille de Klein modélisée dans Solid Edge et rendue dans Keyshot
Une des différences entre modeleur peut être le choix de représentation de certains objets spécifiques :
-
Un cylindre peut être un cône particulier (même équation, demi-angle nul) ou un objet à part
-
Les croisements de congés notamment peuvent être représentés différemment : à base de cylindre, cône, tore et sphère, ou une sphère qui « roule » sur l’arête, ou une surface de Bézier, etc.
La règle Descartes-Euler (ou relation d’Euler)
Toute géométrie représentant un objet réel (manifold) respecte la règle d’Euler. Le théorème de Descartes-Euler (ou relation d’Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de sommets, d’arêtes et de faces dans un polyèdre de genre 0 (c’est-à-dire, intuitivement, un polyèdre « sans trou ») ; tout polyèdre convexe est de genre 0.
S – A + F – 2 = 0 ou S – A + F = 2
F : nombre de Faces
S : Nombre de sommets
A : nombre d’arêtes (Edge)
Quelques conséquences de cette formule :
-
Au moins 3 arêtes sont connectées à chaque sommet
-
Chaque arête appartient à exactement 2 faces
Exemples et contre-exemples :
On peut procéder à la vérification de la propriété pour les cinq solides « platoniciens » :
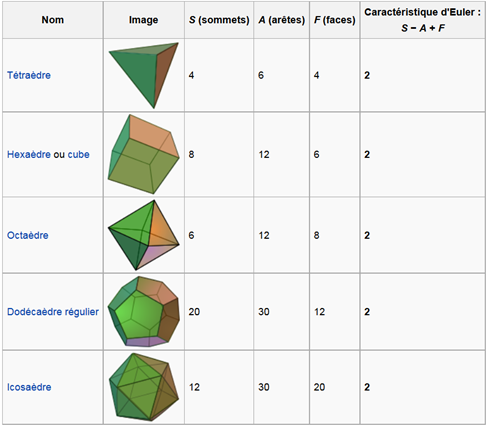
Si les polyèdres ne sont pas du genre 0, on ne peut pas appliquer le théorème de Descartes-Euler. On peut alors trouver pour S ? A + F des valeurs différentes de 2. Ces solides ne sont pas représentables dans Solid Edge en un seul corps :
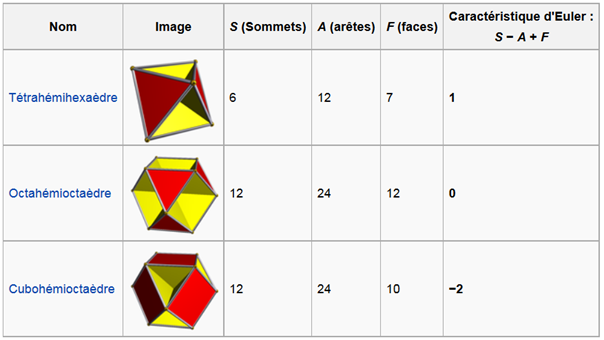
Règle d’Euler pour les pièces avancées
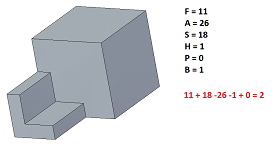
F + S – A – H + 2P =2B
F = Nombre de Faces
S = Nombre de sommets
A = Nombre d’Arêtes
H = Nombre de boucles intérieurs dans les faces (les trous ou protubérances)
P = Nombre de passages ou trous débouchant
B = Nombre de solides distincts (corps ou body)
|
|
|
|
|
|
|
|
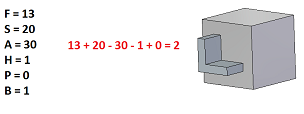
Corps avec une géométrie non manifold
Un cas simple avec un problème :
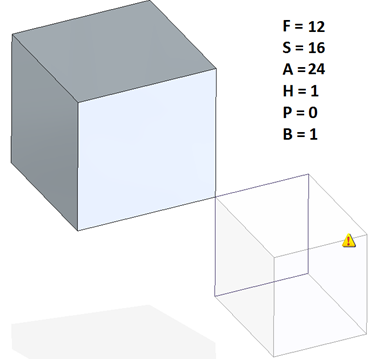
12 + 16 – 24 – 1 + 0 = 3 au lieu de 2 !
Un sommet est partagé par 6 arêtes et 6 faces ! Il faudrait 2 solides différents !
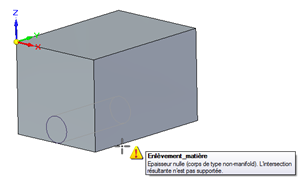
Quelques autres exemples :
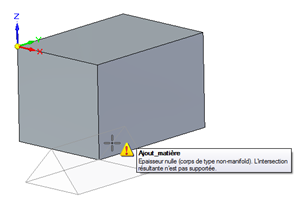
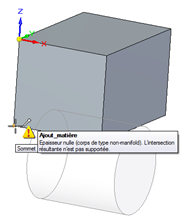
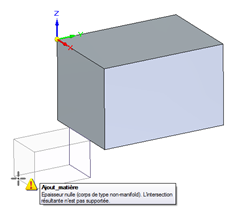
Des différences entre modeleurs
Rappelons que le noyau Parasolid de Solid Edge interdit les représentations de géométrie non manifold pour un seul solide.
Alors pourquoi certains logiciels supportent ces types de géométries ? Même Solid Edge semble le supporter en tôlerie, sur les raccords de coins !
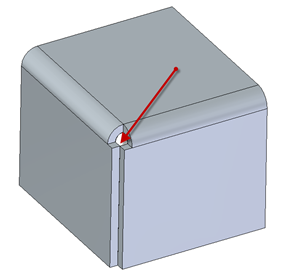
Raccord de coin ouvert, espacement 0
D’autres approches peuvent être prises : dans Solid Edge, nous pouvons depuis ST5 mettre plusieurs corps (volume, solide) dans une pièce. Certains logiciels créent automatiquement un autre corps avec la fonction qui provoque une épaisseur nulle. Mais si le résultat doit être un seul volume, il faudra traiter ce problème avant de faire l’union des corps !
Une autre astuce est de « dégrader » intentionnellement la position des deux arêtes superposées pour contourner ce problème. L’exemple de la tôle ci-dessus joue sur ce paramètre : les arêtes ne sont en fait pas collées ! Sur mon exemple, j’ai une distance de 0.0028284 mm.
Cette notion de précision est d’ailleurs une des nombreuses causes des problèmes d’importations : 2 sommets supposés être au même endroit dans un modeleur « peu précis », et donc considérés comme un seul sommet, seront calculés séparés dans un modeleur « plus précis ». Un sommet à côté d’une arête, l’arête ne se reconstruit pas, les faces qui s’appuient dessus non plus et on retrouve un trou dans le volume ! Un modeleur ou une géométrie manquant de précision posera donc plus de problème à un modeleur précis qu’à un peu précis…
Parasolid travaille en précision absolue : de 1000m à 10-8m, soit 1011 d’intervalle. D’autres modeleurs peuvent travailler en précision glissante : 109 entre la plus petite et la plus grande dimension. Selon la taille de la pièce, on peut être en dessous ou au-dessus du Parasolid.
Ces quelques explications nous donnent un petit aperçu de la complexité du dialogue entre les différentes CAO (sans compter les problèmes « politiques » entre éditeurs…). 2 articles sur Grabcad (Anglais), très simple d’accès, peuvent vous intéresser :
https://blog.grabcad.com/blog/2013/05/14/kernels-why-cad-systems-dont-play-well-with-others/
https://blog.grabcad.com/blog/2013/04/22/a-brief-introduction-to-cad-file-formats/
Ahmed BEN ABDELKADER, Nicolas BERNARD


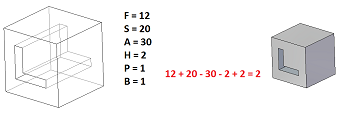
Très intéressant, n’hésitez pas à en publier d’autres du même genre.